Mathematics

วันพฤหัสบดีที่ 5 กันยายน พ.ศ. 2556

การบวกจำนวนเต็ม

การบวกจำนวนเต็มผมจะขอแยกทำให้ดูเป็นกรณีไปน่ะครับ

กรณีที่ 1 การบวกจำนวนเต็มบวกกับจำนวนเต็มบวก

กรณีนี้คงไม่ใช่ปัญหา เพราะกรณีนี้ไม่ยากครับง่ายๆ ตัวอย่างเช่น

1.จงหาผลบวกต่อไปนี้

$\dpi{200}1) 2+3=5$

$\dpi{200}2)Â 5+12=17$

$\dpi{200}20+50=70$

กรณีนี้คงไม่ยากเชื่อว่าทุกคนทำได้น่ะครับ มาดูกรณีต่อไปเลยดีกว่า

กรณีที่ 2 การบวกจำนวนเต็มลบกับจำนวนเต็มลบ

กรณีนี้ก็ไม่ยากเหมือนกันครับ แค่จับหลักได้ก็ง่ายนิดเดียวครับ หลักการของมันมีอยู่ว่า จับตัวเลขบวกกันธรรมดาโดยไม่สนใจเครื่องหมายลบ คำตอบที่ได้เติมลบเข้าไปด้วย คับหลักการมีแค่นี้ เดี๋ยวไปดูตัวอย่างครับ

1.จงหาผลบวกต่อไปนี้

$\dpi{200} 1) (-2)+(-4)=-6$

อธิบายบายวิธีการทำคือ เอาสองไปบวกกับสี่เลย ไม่ต้องไปสนใจเครื่องหมายลบ คำตอบที่ได้คือหก เวลาตอบจริงๆให้เติมลบข้างหน้าเลขหก ก็จะได้เป็น -6 ข้อนี้ตอบ -6 คับ ง่ายป่าว ผมว่าง่ายน่ะ

$\dpi{200}2) (-12)+(-20)=-32$

อธิบายวิธีการทำคือ เอาสิบสองไปบวกกับยี่สิบเลย ไม่ต้องไปสนใจเครื่องหมายลบ คำตอบที่ได้คือสามสิบสอง แต่เวลาตอบจริงๆให้เติมลบข้างหน้าเลขสามสิบสองด้วยก็จะได้คำตอบข้อนี้เป็น -32 คับ

$\dpi{200}3) (-49)+(-11)=-60$ วิธีการทำเหมือนข้อที่ผ่านมาน่ะครับ

$\dpi{200}4)(-157)+(-102)=-259$

คงไม่ต้องยกตัวอย่างเยอะน่ะครับ จับหลักการได้ก็ไม่ยากเลยน่ะครับ

สรุปให้อีกทีน่ะครับ ถ้าเป็นการบวกกันระหว่างจำนวนเต็มลบกับจำนวนเต็มลบ ให้นำจำนวนสองจำนวนนั้นบวกกันเลยครับโดยที่ไม่ต้องสนใจเครื่องหมาย แต่เวลาตอบจริงๆให้ใส่เครื่องหมายลบหน้าคำตอบด้วยครับ หลักการก็มีแค่นี้ครับง่ายๆ

กรณีที่ 3 การบวกจำนวนเต็มลบกับจำนวนเต็มบวก (ตัวหนึ่งเป็นจำนวนเต็มลบแต่อีกตัวหนึ่งเป็นจำนวนเต็มบวก)

กรณีนี้ผมว่ามันก็ไม่ยากน่ะ สรุปก็คือไม่ยากทั้ง 3 กรณี หลักการของมันมีดังนี้คือ ขั้นแรกเราไม่ต้องไปสนใจเครื่องหมายหน้าตัวเลขมันจะเป็นลบหรือเป็นบวกช่างมันครับ ให้เรานำจำนวนที่มีค่ามากตั้ง ลบออกด้วยจำนวนที่มีค่าน้อยกว่า ที่นี้คำตอบที่ได้มันจะเป็นบวกหรือเป็นลบให้เป็นไปตามตัวที่มีค่ามากกว่า ถ้าตัวมากติดลบคำตอบต้องติดลบ ถ้าตัวมากเป็นบวกคำตอบก็ต้องเป็นบวกด้วยครับ อธิบายมาซะยืดยาว ผมว่าหลายๆคนคงอ่านแล้วงง งั้นไปดูตัวอย่างประกอบครับ

1.จงหาผลบวกต่อไปนี้

$\dpi{200}1) (-4)+1$

อธิบายวิธีการทำข้อนี้คือ ขั้นแรกเราไม่ต้องสนใจเครื่องหมายหน้าตัวเลขครับว่าจะเป็นลบหรือบวกช่างหัวมันครับ ให้นำจำนวนที่มีค่ามากตั้งแล้วลบออกด้วยจำนวนที่น้อยกว่า ในที่นี้ คือนำ 4-1=3 คำตอบที่ได้คือสาม ยังไม่ใช่คำตอบจริงๆน่ะครับเราต้องมาดูเครื่องหมายหน้าเลขสามอีกว่าจะเป็นบวกหรือเป็นลบ การดูก็คือ พิจารณา 4 กับ 1 ว่าตัวไหนมีค่ามากกว่ากัน

แน่นอน 4 มีค่ามากกว่าอยู่แล้ว คำตอบที่ได้จะต้องมีเครืองหมายเหมือนกับตัวที่มากกว่า ตัวที่มากว่าติดลบ ดังนั้นคำต้องติดลบด้วย ข้อนี้ตอบ -3 คับ จึงได้ว่า

$\dpi{200} (-4)+1=-3$

$\dpi{200}2) 9+(-20)$

อธิบายวิธีการทำคือ นำ ตัวมากลบตัวน้อยคือ 20-9=11 สิบเอ็ดยังไม่ใช่คำตอบจริงๆครับ ที่นี้ดูว่า 20 กับ 9 อะไรมากกว่ากัน แน่นอน 20 มากกว่าและหน้ายี่สิบมีเครื่องหมายติดลบด้วย ดังนั้นข้อนี้ตอบ -11 คับ จึงได้ว่า

$\dpi{200} 9+(-20)=-11$

$\dpi{200}3) 13+(-14)$

อธิบายวิธีการทำคือ เอาจำนวนที่มากตั้งลบด้วยจำนวนที่น้อยกว่าไม่ต้องสนใจเครื่องหมาย นั่นคือ 14-13=1 ดูที่โจทย์ตัวที่มากคือ 14 คำตอบจะมีเครื่องหมายตามตัวที่มาก ดังนั้นข้อนี้ตอบ -1 จึงได้ว่า

$\dpi{200} 13+(-14)=-1$

$\dpi{200} 4) 28+(-18)$

วิธีการทำก็คือ นำจำนวนมากลบออกด้วยจำนวนที่น้อยกว่า นั้่นคือ 28-18=10 ต่อไปดูว่า 28 กับ 18 อะไรมีค่ามากกว่ากันแน่นอน 28 มากว่า คำตอบจะมีเครืองหมายตามตัวที่มากกว่าตัวมากคือ 28 เป็นบวก คำตอบก็ต้องออกมาเป็นบวกด้วยนั้นตอบ 10 นั่นเอง จึงได้ว่า

$\dpi{200}28+(-18)=10$

$\dpi{200} 5)Â (-49)+12$

วิธีการทำข้อนี้คือ นำจำนวนมากลบออกด้วยจำนวนที่น้อยกว่า นั่นคือ 49-12=37 (ยังไม่ต้องสนใจเครื่องหมายครับ) ต่อไปดูที่โจทย์ว่า 49 กับ 12 อะไรมีค่ามากกว่ากัน แน่นอน 49 มีค่ามากกว่า คำตอบจะมีเครื่องหมายตามตัวที่มากคือ 49 ตัวที่มากมีเครื่องหมายเป็นลบอยู่ข้างหน้า นั่นคือข้อนี้ ตอบ -37 คับ จึงได้ว่า

$\dpi{200}(-49)+12=-37$

$\dpi{200} 6)Â (-18)+78$

วิธีการทำข้อนี้คือ นำตัวมากลบออกด้วยตัวน้อยนั่นคือ 78-18=60 ต่อไปดูที่โจทย์ว่า 18 กับ 78 อะไรมีค่ามากกว่ากันแน่ะนอน 78 มากกว่า คำตอบจะมีเครืองหมายตามตัวที่มากคือ 78 ตัวที่มากมีเครื่องหมายเป็นบวกดังนั้นคำตอบต้องเป็นบวกด้วย นั้นคือข้อนี้ตอบ 60 จึงได้ว่า

$\dpi{200}Â Â (-18)+78=60$

http://www.mathpaper.net/index.php/2013-01-15-06-33-22/233-2013-04-30-10-00-28

เศษส่วน

นทางคณิตศาสตร์ เศษส่วน คือความสัมพันธ์ตามสัดส่วนระหว่างชิ้นส่วนของวัตถุหนึ่งเมื่อเทียบกับวัตถุทั้งหมด เศษส่วนประกอบด้วยตัวเศษ (numerator) หมายถึงจำนวนชิ้นส่วนของวัตถุที่มี และตัวส่วน (denominator) หมายถึงจำนวนชิ้นส่วนทั้งหมดของวัตถุนั้น ตัวอย่างเช่น 34 อ่านว่า เศษสามส่วนสี่ หรือ สามในสี่ หมายความว่า วัตถุสามชิ้นส่วนจากวัตถุทั้งหมดที่แบ่งออกเป็นสี่ส่วนเท่าๆ กัน นอกจากนั้น การแบ่งวัตถุสิ่งหนึ่งออกเป็นศูนย์ส่วนเท่า ๆ กันนั้นเป็นไปไม่ได้ ดังนั้น 0 จึงไม่สามารถเป็นตัวส่วนของเศษส่วนได้ (ดูเพิ่มที่ การหารด้วยศูนย์)

เศษส่วนเป็นตัวอย่างชนิดหนึ่งของอัตราส่วน ซึ่งเศษส่วนแสดงความสัมพันธ์ระหว่างชิ้นส่วนย่อยต่อชิ้นส่วนทั้งหมด ในขณะที่อัตราส่วนพิจารณาจากปริมาณของสองวัตถุที่แตกต่างกัน (ดังนั้น 34 อาจไม่เท่ากับ 3 : 4) และเศษส่วนนั้นอาจเรียกได้ว่าเป็นผลหาร(quotient) ของจำนวน ซึ่งปริมาณที่แท้จริงสามารถคำนวณได้จากการหารตัวเศษด้วยตัวส่วน ตัวอย่างเช่น 34 คือการหารสามด้วยสี่ ได้ปริมาณเท่ากับ 0.75 ในทศนิยม หรือ 75% ในอัตราร้อยละ

การเขียนเศษส่วน ให้เขียนแยกออกจากกันด้วยเครื่องหมายทับหรือ ซอลิดัส (solidus) แล้ววางตัวเศษกับตัวส่วนในแนวเฉียง เช่น ¾ หรือคั่นด้วยเส้นแบ่งตามแนวนอนเรียกว่า วิงคิวลัม (vinculum) เช่น 34 ในบางกรณีอาจพบเศษส่วนที่ไม่มีเครื่องหมายคั่น อาทิ ³₄ บนป้ายจราจรในบางประเทศ

http://th.wikipedia.org/wiki/%E0%B9%80%E0%B8%A8%E0%B8%A9%E0%B8%AA%E0%B9%88%E0%B8%A7%E0%B8%99

สมการ

สมการ หมายถึงประโยคสัญลักษณ์ทางคณิตศาสตร์ ที่ใช้แสดงว่าสองสิ่งเหมือนกัน หรือเทียบเท่ากัน ที่เชื่อมด้วยเครื่องหมายเท่ากับ ดังตัวอย่าง

$2 + 3 = 5\,$

สมการมักใช้เป็นการกำหนดสภาวะความเท่ากันของสองนิพจน์ที่มีตัวแปรอย่างน้อยหนึ่งตัว ตัวอย่างเช่น เมื่อเราให้ค่าใดๆ กับ $x$ สมการนี้จะเป็นจริงเสมอ

$x - x = 0\,$

ทั้งสองสมการข้างต้นเป็นตัวอย่างหนึ่งของสมการที่เป็นเอกลักษณ์ ซึ่งหมายความว่า สมการจะเป็นจริงโดยไม่ต้องมีการแทนค่าใดๆ ลงในตัวแปร สำหรับสมการต่อไปนี้ไม่ได้เป็นเอกลักษณ์

$x + 1 = 2\,$

สมการข้างบนนี้จะไม่เป็นจริงเมื่อแทนค่าอื่นใด แต่จะเป็นจริงแค่เพียงค่าเดียว เราเรียกค่าที่ทำให้สมการเป็นจริงนั้นว่า รากของสมการ สำหรับรากของสมการดังกล่าวคือ 1 ดังนั้น สมการนี้สามารถเป็นจริงได้ ขึ้นอยู่กับค่าของ $x$ เรียก x ที่ทำให้สมการเป็นจริงว่า "คำตอบของสมการ" นั่นคือการแก้สมการจึงเป็นการหาคำตอบของสมการวิธีหนึง เช่น 5 - x = 1 มีคำตอบของสมการ คือ 4

หลักการแก้สมการ[แก้]

การแก้สมการให้ย้ายข้างดังนี้

1. ถ้าตัวเลขในฝั่งซ้ายมีค่าเป็นบวก และฝั่งขวามีค่าเป็นบวกและมากกว่าฝั่งซ้ายให้ย้ายไปลบได้เลย เช่น

$A + 56 = 57\,$

$A = 57 - 56\,$

$A = 1\,$

คุณสมบัติ[แก้]

ถ้าสมการในพีชคณิตสามารถเป็นจริงได้ การกระทำต่อไปนี้ก็สามรถทำให้ทั้งสองข้างเท่ากัน เราเรียกว่า สมบัติการเท่ากัน

ปริมาณใดๆ สามารถบวกทั้งสองข้างของสมการได้
ปริมาณใดๆ สามารถลบทั้งสองข้างของสมการได้
ปริมาณใดๆ สามารถคูณทั้งสองข้างของสมการได้
ปริมาณใดๆ ที่ไม่เท่ากับศูนย์ สามารถหารทั้งสองข้างของสมการได้
โดยทั่วไป ฟังก์ชันใดๆ สามารถนำไปใช้กับทั้งสองข้างของสมการได้ (ยกเว้นบางฟังก์ชันที่ต้องกำหนดเงื่อนไขก่อนนำไปใช้ เช่น ฟังก์ชันตรีโกณมิติ ฟังก์ชันเอกซโพเนนเชียล เป็นต้น)http://th.wikipedia.org/wiki/%E0%B8%AA%E0%B8%A1%E0%B8%81%E0%B8%B2%E0%B8%A3

สูตรการหาพื้นที่รูปสี่เหลี่ยม

สูตรการหาพื้นที่รูปสี่เหลี่ยมต่างๆ

สูตรมาตรฐานของสามเหลี่ยม

สามเหลี่ยม=เศษหนึ่งส่วนสอง คูณ สูง คูณฐาน

สูตรต่างๆของการหาพื้นที่รูปสี่เหลี่ยม

ความยาวรอบรูปของรูปสี่เหลี่ยมใดใด=ผลบวกของด้านทุกด้าน

สี่เหลี่ยมผืนผ้า=กว้าง คูณ ยาว

สี่เหลี่ยมจัตุรัส=ด้าน คูณ ด้าน

สี่เหลี่ยมด้านขนาน=สูง คูณ ฐาน

สี่เหลี่ยมคางหมู=เศษหนึ่งส่วนสอง คูณ ผลบวกด้านคู่ขนาน คูณ สูง

สี่เหลี่ยมขนมเปียกปูน=เศษหนึ่งส่วนสอง คูณ ผลคูณของเส้นทแยงมุม

สี่เหลี่ยมใดใด=เศษหนึ่งส่วนสอง คูณ เส้นทแยงมุม คูณ ผลบวกของเส้นกิ่ง

สี่เหลี่ยมรูปว่าว=เศษหนึ่งส่วนสอง คูณ ผลคูณของhttp://www.tlcthai.com/education/knowledge-online/content-edu/16167.html

การคูณ

การคูณ คือการดำเนินการทางคณิตศาสตร์อย่างหนึ่ง ทำให้เกิดการเพิ่มหรือลดจำนวนจำนวนหนึ่งเป็นอัตรา การคูณเป็นหนึ่งในสี่ของการดำเนินการพื้นฐานของเลขคณิตมูลฐาน (การดำเนินการอย่างอื่นได้แก่ การบวก การลบ และการหาร) การคูณสามารถนิยามบนจำนวนธรรมชาติว่าเป็นการบวกที่ซ้ำๆ กัน ตัวอย่างเช่น 4 คูณด้วย 3 (หรือเรียกโดยย่อว่า 4 คูณ 3) หมายถึงการบวกจำนวน 4 เข้าไป 3 ชุด ดังนี้ สำหรับการคูณของจำนวนตรรกยะ (เศษส่วน) และจำนวนจริง ก็นิยามโดยกรณีทั่วไปที่เป็นระบบของแนวความคิดพื้นฐานดังกล่าว การคูณอาจมองได้จากการนับวัตถุที่จัดเรียงกันเป็นรูปสี่เหลี่ยมผืนผ้า (สำหรับจำนวนธรรมชาติ) หรือการหาพื้นที่ของรูปสี่เหลี่ยมผืนผ้าโดยการหนดความยาวของด้านมาให้ (สำหรับจำนวนทั่วไป) ส่วนกลับของการคูณคือการหาร ในเมื่อ 4 คูณด้วย 3 เท่ากับ 12 ดังนั้น 12 หารด้วย 3 ก็จะเท่ากับ 4 เป็นต้น การคูณสามารถนิยามให้ขยายไปบนจำนวนชนิดอื่นเช่นจำนวนเชิงซ้อน และมีโครงสร้างที่เป็นนามธรรมมากขึ้นเช่นเมทริกซ์ โดยทั่วไปการคูณสามารถเขียนโดยใช้เครื่องหมายคูณ (×) ระหว่างจำนวนทั้งสอง (ในรูปแบบสัญกรณ์เติมกลาง) ตัวอย่างเช่น (อ่านว่า 2 คูณ 3 เท่ากับ 6) อย่างไรก็ตามก็ยังมีการใช้สัญกรณ์อื่นๆ แทนการคูณโดยทั่วไป อาทิ • ใช้จุดกลาง (•) หรือไม่ก็มหัพภาค (.) อย่างใดอย่างหนึ่ง เช่น 5 • 2 หรือ 5 . 2 การใช้จุดกลางเป็นมาตรฐานในสหรัฐอเมริกา สหราชอาณาจักร และประเทศอื่นๆ ที่ใช้มหัพภาคเป็นจุดทศนิยม แต่ในบางประเทศที่ใช้จุลภาคเป็นจุดทศนิยม จะใช้มหัพภาคเป็นการคูณแทน • ใช้ดอกจัน (*) เช่น 5*2 มักใช้ในภาษาโปรแกรมเพราะเครื่องหมายนี้ปรากฏอยู่บนทุกแป้นพิมพ์ และสามารถดูได้ง่ายบนจอมอนิเตอร์รุ่นเก่า การใช้เครื่องหมายนี้แทนการคูณเริ่มมีขึ้นตั้งแต่ภาษาฟอร์แทรน • ในพีชคณิต การคูณที่เกี่ยวกับตัวแปรมักจะเขียนให้อยู่ติดกัน เรียกว่า juxtaposition ตัวอย่างเช่น xy หมายถึง x คูณ y และ 5x หมายถึง 5 คูณ x เป็นต้น สัญกรณ์เช่นนี้สามารถใช้กับจำนวนที่ครอบด้วยวงเล็บ เช่น หรือ ก็จะหมายถึง 5 คูณ 2 • ในการคูณเมทริกซ์ มีความแตกต่างระหว่างการใช้สัญลักษณ์กากบาทกับจุด กากบาทใช้แทนการคูณเวกเตอร์ ในขณะที่จุดใช้แทนการคูณสเกลาร์ ดังนั้นการตั้งชื่อเรียกจึงแตกต่างกันคือผลคูณไขว้และผลคูณจุดตามลำดับ จำนวนที่ถูกคูณโดยทั่วไปเรียกว่า ตัวประกอบ (factor) หรือ ตัวตั้งคูณ (multiplicand) ส่วนจำนวนที่นำมาคูณเรียกว่า ตัวคูณ (multiplier) ตัวคูณของตัวแปรหรือนิพจน์ในพีชคณิตจะเรียกว่า สัมประสิทธิ์ (coefficient) ซึ่งจะเขียนไว้ทางซ้ายของตัวแปรหรือนิพจน์ เช่น 3 เป็นสัมประสิทธิ์ของ 3xy2 ผลลัพธ์ที่เกิดจากการคูณเรียกว่า ผลคูณ (product) หรือเรียกว่า พหุคูณ (multiple) ของตัวประกอบแต่ละตัวที่เป็นจำนวนเต็ม ตัวอย่างเช่น 15 คือผลคูณของ 3 กับ 5 และในขณะเดียวกัน 15 ก็เป็นทั้งพหุคูณของ 3 และพหุคูณของ 5 ด้วย

สูตรการหาพื้นที่รูปสี่เหลี่ยม

รูปสามเหลี่ยม (อังกฤษ: triangle) เป็นหนึ่งในรูปร่างพื้นฐานในเรขาคณิต คือรูปหลายเหลี่ยมซึ่งมี 3 มุมหรือจุดยอด และมี 3 ด้านหรือขอบที่เป็นส่วนของเส้นตรง รูปสามเหลี่ยมที่มีจุดยอด A, B, และ C เขียนแทนด้วย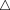

ABC

ในเรขาคณิตแบบยุคลิด จุด 3 จุดใดๆ ที่ไม่อยู่ในเส้นตรงเดียวกัน จะสามารถสร้างรูปสามเหลี่ยมได้เพียงรูปเดียว และเป็นรูปที่อยู่บนระนาบเดียว (เช่นระนาบสองมิติ)

แบ่งตามความยาวของด้าน[แก้]

รูปสามเหลี่ยมด้านเท่า (equilateral) มีด้านทุกด้านยาวเท่ากัน รูปสามเหลี่ยมด้านเท่าเป็นรูปหลายเหลี่ยมมุมเท่า นั่นคือมุมภายในทุกมุมจะมีขนาดเท่ากัน คือ 60° และเป็นรูปหลายเหลี่ยมปกติ ^[1]
รูปสามเหลี่ยมหน้าจั่ว (isosceles) มีด้านสองด้านยาวเท่ากัน (ตามความหมายเริ่มแรกโดยยุคลิด ถึงแม้ว่ารูปสามเหลี่ยมด้านเท่าจะสามารถจัดว่าเป็นรูปสามเหลี่ยมหน้าจั่วได้ด้วย เพราะมีด้านที่ยาวเท่ากันอย่างน้อยสองด้าน) และมีมุมสองมุมขนาดเท่ากัน คือมุมที่ไม่ได้ประกอบด้วยด้านที่เท่ากันทั้งสอง ^[2]
รูปสามเหลี่ยมด้านไม่เท่า (scalene) ด้านทุกด้านจะมีความยาวแตกต่างกัน มุมภายในก็มีขนาดแตกต่างกันด้วย ^[3]


รูปสามเหลี่ยมด้านเท่า	รูปสามเหลี่ยมหน้าจั่ว	รูปสามเหลี่ยมด้านไม่เท่า

แบ่งตามมุมภายใน[แก้]

รูปสามเหลี่ยมมุมฉาก (right, right-angled, rectangled) มีมุมภายในมุมหนึ่งมีขนาด 90° (มุมฉาก) ด้านที่อยู่ตรงข้ามกับมุมฉากเรียกว่า ด้านตรงข้ามมุมฉาก ซึ่งเป็นด้านที่ยาวที่สุดในรูปสามเหลี่ยม อีกสองด้านเรียกว่า ด้านประกอบมุมฉาก ความยาวด้านของรูปสามเหลี่ยมมุมฉากสัมพันธ์กันตามทฤษฎีบทพีทาโกรัส นั่นคือกำลังสองของความยาวของด้านตรงข้ามมุมฉาก c จะเท่ากับผลบวกของกำลังสองของด้านประกอบมุมฉาก a, b เขียนอย่างย่อเป็น $a^2 + b^2 = c^2$ ดูเพิ่มเติมที่ รูปสามเหลี่ยมมุมฉากพิเศษ
รูปสามเหลี่ยมมุมเฉียง (oblique) ไม่มีมุมใดเป็นมุมฉาก ซึ่งอาจหมายถึงรูปสามเหลี่ยมมุมป้านหรือรูปสามเหลี่ยมมุมแหลม
รูปสามเหลี่ยมมุมป้าน (obtuse) มีมุมภายในมุมหนึ่งมีขนาดใหญ่กว่า 90° (มุมป้าน)
รูปสามเหลี่ยมมุมแหลม (acute) มุมภายในทุกมุมมีขนาดเล็กกว่า 90° (มุมแหลม) รูปสามเหลี่ยมด้านเท่าเป็นรูปสามเหลี่ยมมุมแหลม แต่รูปสามเหลี่ยมมุมแหลมทุกรูปไม่ได้เป็นรูปสามเหลี่ยมด้านเท่า


รูปสามเหลี่ยมมุมฉาก	รูปสามเหลี่ยมมุมป้าน	รูปสามเหลี่ยมมุมแหลม
	$\underbrace{\qquad \qquad \qquad \qquad \qquad \qquad}_{}$ รูปสามเหลี่ยมมุมเฉียง (ไม่มีมุมฉาก)